Code
from qiskit import QuantumCircuit
from math import piThe quantum Fourier transform
The Fourier transform is a beautiful function with many important applications. There is a wonderful introduction to the Fourier transform by 3 Blue 1 Brown that is well worth watching. The following is a description of the quantum Fourier transform (QFT). After defining a closed formula for QFT, I will explain how to build the QFT circuit using a recursive formula. In the end, I will prove that the closed formula and recursive formula agree. All the quantum circuits in this post are created with qiskit.
\(n\)-qubit representations of integers
Fix a positive integer \(n\) and let \(N=2^n\) denote the dimension of the \(n\)-qubit state space. In what follows, given an integer \(0\leq a< N\) we write \(|a\rangle\) for the state vector corresponding to the \(a\)-th standard basis vector. In other words, \(|a\rangle=|a_{n-1}\cdots a_1a_0\rangle\) where each \(a_i\in\{0,1\}\) and \(a=\sum\limits_{k=0}^{n-1}a_k2^k\). For example, when \(n=3\) we have
\[\begin{align*} |0\rangle &= |000\rangle, & |1\rangle &= |001\rangle, \\ |2\rangle &= |010\rangle, & |3\rangle &= |011\rangle, \\ |4\rangle &= |100\rangle, & |5\rangle &= |101\rangle, \\ |6\rangle &= |110\rangle, & |7\rangle &= |111\rangle. \\ \end{align*}\]
This is just the usual binary representation of integers, but with qubits. I like to refer to \(|a\rangle\) as the (standard) \(n\)-qubit representation of the integer \(a\).
A closed formula for QFT
The quantum Fourier transform \(QFT_n\) is define on the \(n\)-qubit representation of \(a\) by \[ QFT_n|a\rangle = \dfrac{1}{\sqrt{N}}\sum_{b=0}^{N-1}e^{2\pi i a b/N}|b\rangle. \tag{1}\]
Example: \(QFT_1\)
When \(n=1\) (so that \(N=2\)) the closed formula above shows that \(QFT_1\) maps
\[\begin{align*} |0\rangle & \mapsto \dfrac{1}{\sqrt{2}}\left(|0\rangle + |1\rangle\right)\\ |1\rangle & \mapsto \dfrac{1}{\sqrt{2}}\left(|0\rangle - |1\rangle\right) \end{align*}\]
This is the same mapping given by our beloved Hadamard gate, so \(QFT_1=H\).
Example: \(QFT_2\)
When \(n=2\) (so that \(N=4\)) the closed formula shows that \(QFT_2\) maps
\[\begin{align*} |0\rangle & \mapsto \dfrac{1}{2}\left(|0\rangle + |1\rangle + |2\rangle + |3\rangle\right)\\ |1\rangle & \mapsto \dfrac{1}{2}\left(|0\rangle + i|1\rangle -|2\rangle - i|3\rangle\right)\\ |2\rangle & \mapsto \dfrac{1}{2}\left(|0\rangle - |1\rangle + |2\rangle - |3\rangle\right)\\ |3\rangle & \mapsto \dfrac{1}{2}\left(|0\rangle - i|1\rangle - |2\rangle + i|3\rangle\right) \end{align*} \tag{2}\]
Equivalently, expanding the above states into qubits we see \(QFT_2\) maps
\[\begin{align*} |00\rangle & \mapsto \dfrac{1}{2}\left(|00\rangle + |01\rangle + |10\rangle + |11\rangle\right)\\ |01\rangle & \mapsto \dfrac{1}{2}\left(|00\rangle + i|01\rangle -|10\rangle - i|11\rangle\right)\\ |10\rangle & \mapsto \dfrac{1}{2}\left(|00\rangle - |01\rangle + |10\rangle - |11\rangle\right)\\ |11\rangle & \mapsto \dfrac{1}{2}\left(|00\rangle - i|01\rangle - |10\rangle + i|11\rangle\right) \end{align*} \tag{3}\]
The QFT circuit
CP-chains
One of the building blocks (subcircuits) of the QFT circuit consists of a composition of controlled phase gates. We will call these subcircuits CP-chains. In the following we will describe these CP-chains and give an explicit formula for how they map qubit states.
Phase gates
We will write \(P_\phi\) for the P-gate, which depends on a parameter \(\phi\), that maps qubits as follows
\[\begin{align*} |0\rangle & \mapsto |0\rangle\\ |1\rangle & \mapsto e^{\phi i} |1\rangle \end{align*}\] In other words, a P-gate applies a relative phase change to the \(|1\rangle\) component of a qubit. If you prefer to describe gates by matrices, then \[P_\phi=\begin{pmatrix} 1 & 0\\ 0 & e^{\phi i} \end{pmatrix}\]
Note that we can get a little clever and write the P-gate mapping as \[P_\phi: |q\rangle \mapsto e^{q\phi i}|q\rangle\] where \(q\in\{0, 1\}\). The P-gate \(P_{\pi/2}\) is pictured as follows:
Code
qc = QuantumCircuit(1)
qc.p(pi/2, 0)
qc.draw(output='mpl')
Controlled phase gates
Using the cleverness above, a controlled P-gate will map \[CP_\phi: |q_1q_0\rangle \mapsto e^{q_1q_0\phi i}|q_1q_0\rangle.\]
The controlled P-gate \(CP_{\pi/2}\) is drawn as follows:
Code
qc = QuantumCircuit(2)
qc.cp(pi/2, 0, 1)
qc.draw(output='mpl', reverse_bits=True)
A chain of controlled phase gates
Suppose we are concerned with a \((n+1)\)-qubit state space. Consider \(n\) CP-gates: \(CP_{\pi/2^k}\) between the \(n\)-th and \((n-k)\)-th qubit for each \(1\leq k\leq n\). For example, when \(n=4\) the composition of these four CP-gates is the following:
Code
def cpc(n):
qc = QuantumCircuit(n, name=' CPC ')
for k in range(1, n):
qc.cp(pi/(2**k), n-1, n-1-k)
return qc
cpc(5).draw(output='mpl', reverse_bits=True)
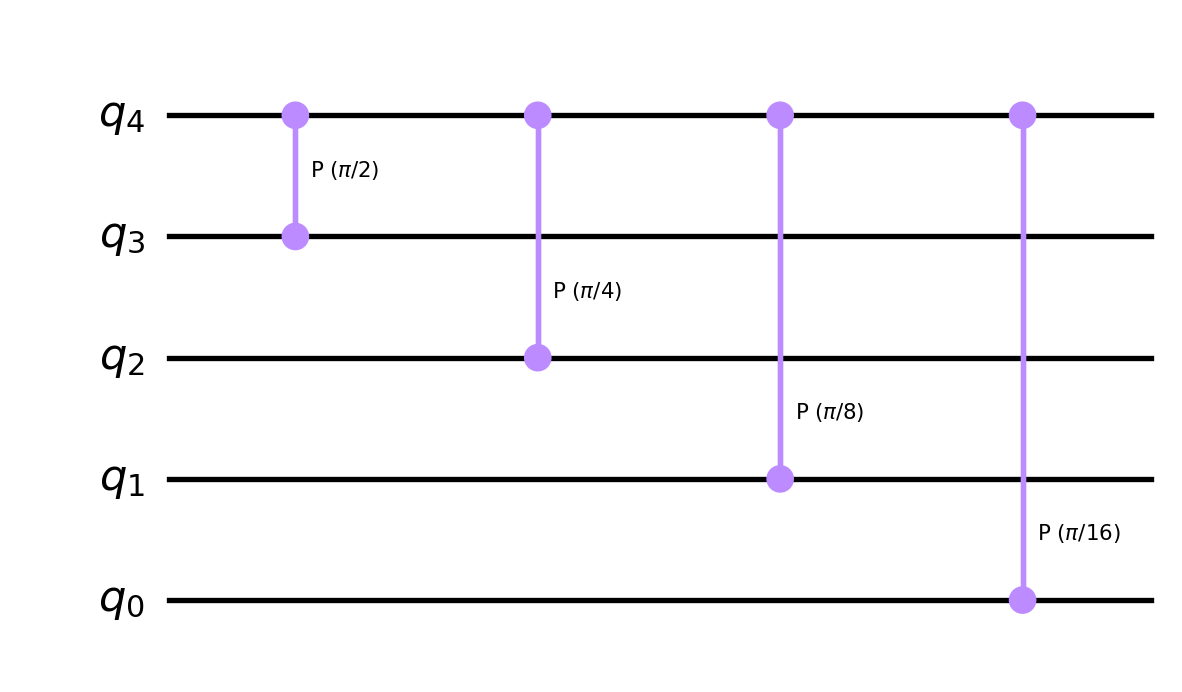
I don’t know a standard name for the circuit above, so I’ll refer to the composition of these \(n\) CP-gates as the CP-chain, denoted \(CPC_{n+1}\). For example, the circuit drawn above is \(CPC_5\). Based on the mapping of \(CP_\phi\) given above, it follows that the CP-chain maps \(|a\rangle=|a_n\cdots a_1a_0\rangle\), the \((n+1)\)-qubit representation of an integer \(0\leq a< 2^{n+1}\), as follows: \[CPC_{n+1}:|a_na_{n-1}\cdots a_1a_0\rangle \mapsto \prod\limits_{k=1}^ne^{\frac{\pi i a_na_{n-k}}{2^k}}|a_na_{n-1}\cdots a_1a_0\rangle\] To simplify the expression above, it will be useful to let \(a'\) denote the integer with \(n\)-qubit representation \(|a'\rangle=|a_{n-1}\cdots a_1a_0\rangle\) so that \(|a\rangle=|a_n\rangle\otimes|a'\rangle\). With this notation, the amplitude above simplifies as \[\begin{align*} \prod\limits_{k=1}^ne^{\frac{\pi i a_na_{n-k}}{2^k}} & =e^{\sum_{k=1}^n\frac{\pi i a_na_{n-k}}{2^k}} \\ & =e^{\frac{\pi i a_n}{2^n}\sum_{k=1}^na_{n-k}2^{n-k}} \\ & =e^{\frac{\pi i a_n}{2^n}\sum_{k=0}^{n-1}a_{k}2^{k}} \\ & =e^{\frac{\pi i a_na'}{2^n}}. \\ \end{align*}\] Thus, the CP-chain mapping can be written as \[ CPC_{n+1}:|a_n\rangle\otimes|a'\rangle \mapsto e^{\frac{\pi i a_na'}{2^n}} |a_n\rangle\otimes|a'\rangle. \tag{4}\]
Reverse circuits
Reversing the order of the qubits is another component of the QFT circuit. Reversing qubits can easily be accomplished using swap gates. The swap gate, pictured below, maps \(|q_1q_0\rangle\to|q_0q_1\rangle\).
Code
qc = QuantumCircuit(2)
qc.swap(0, 1)
qc.draw(output='mpl', reverse_bits=True)
We let \(Rev_n\) for the \(n\)-qubit gate that reverses the qubit order. For example, \(Rev_2\) is the swap gate above. To obtain \(Rev_n\), one simply swaps the first and last qubit, the second and second to last qubit, and so on. For example, the following is \(Rev_7\):
Code
def rev(n):
qc = QuantumCircuit(n, name=' Rev ')
for i in range(n//2):
qc.swap(i, n-i-1)
return qc
rev(7).draw(output='mpl', reverse_bits=True)
A recursive formula for QFT
We are now in position to state recursive formula for the QFT that will allow use to build the QFT circuits:
\[ QFT_{n+1} = Rev_{n+1}\circ (I\otimes (Rev_n\circ QFT_n))\circ CPC_{n+1}\circ(H\otimes I^{\otimes n}) \tag{5}\]
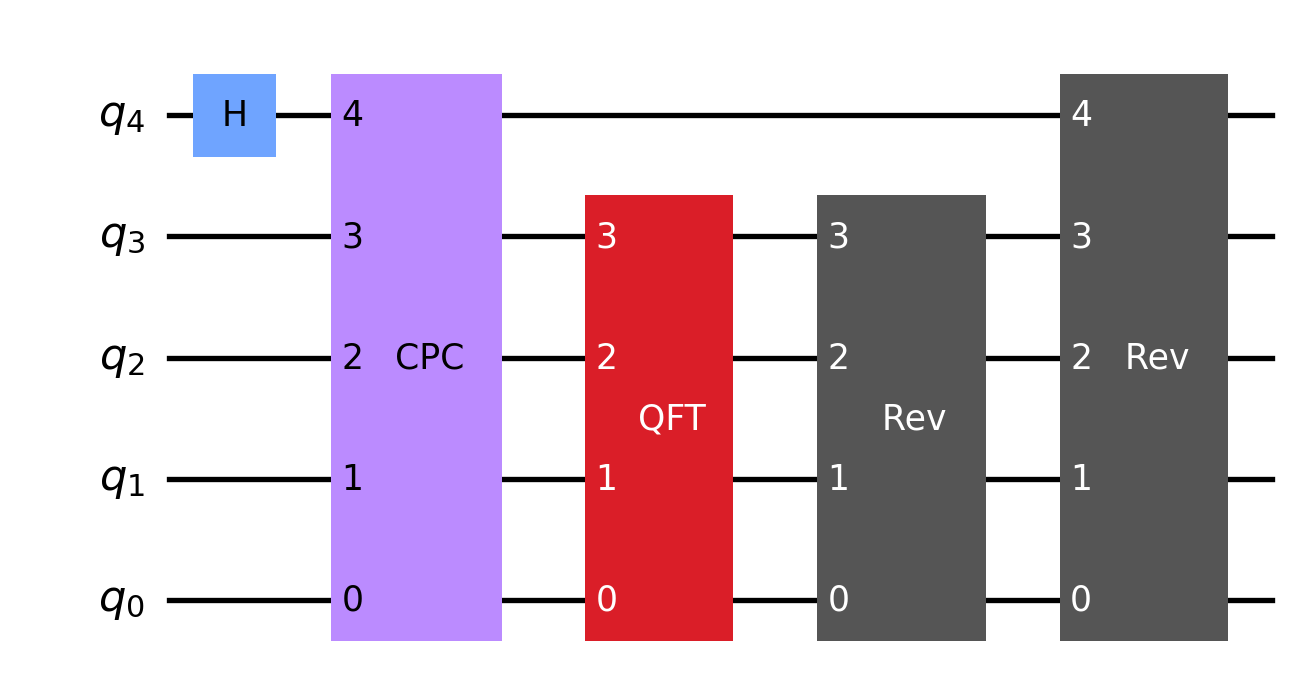
The formula above may be easier to visualize using circuits. Here is the recursively defined QFT circuit:
Code
def qft(n):
qc = QuantumCircuit(n, name=f' QFT ')
qc.h(n-1)
if n == 1:
return qc
qc.append(cpc(n), range(n))
qc.append(qft(n-1), range(n-1))
qc.append(rev(n-1), range(n-1))
qc.append(rev(n), range(n))
return qc
qft(5).draw(output='mpl', reverse_bits=True, style={
"displaycolor": {
" Rev ": [ # gate name
"#555555", # box color (grey)
"#FFFFFF" # box text color (white)
],
" QFT ": [ # gate name
"#da1e28", # box color (red)
"#FFFFFF" # box text color (white)
],
}})
The QFT circuit
Starting with \(QFT_1=H\), the recursive formula 5 can be used to build all the QFT circuits in terms of H, CP, and swap gates. For example, here is \(QFT_2\):
Code
qc = QuantumCircuit(2)
qc.h(1)
qc.cp(pi/2, 1, 0)
qc.h(0)
qc.swap(0,1)
qc.draw(output='mpl', reverse_bits=True)
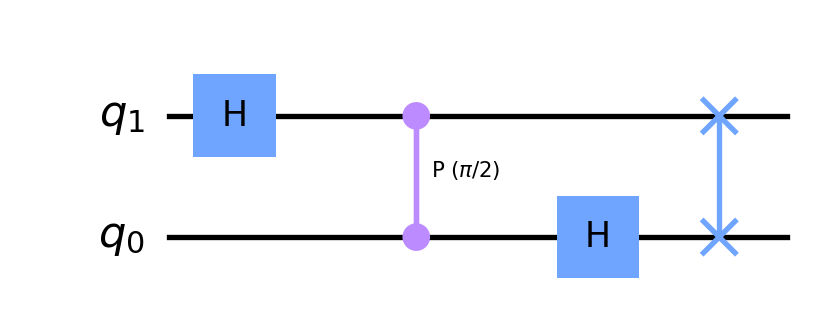
Plugging this into the recursive formula 5 gives us \(QFT_3\). After simplifying (Rev-gates are their own inverses) and expanding the CPC and Rev gates into CP and swap gates, we get the following for \(QFT_3\):
Code
qc = QuantumCircuit(3)
qc.h(2)
qc.cp(pi/2, 2, 1)
qc.cp(pi/4, 2, 0)
qc.h(1)
qc.cp(pi/2, 1, 0)
qc.h(0)
qc.swap(0,2)
qc.draw(output='mpl', reverse_bits=True)
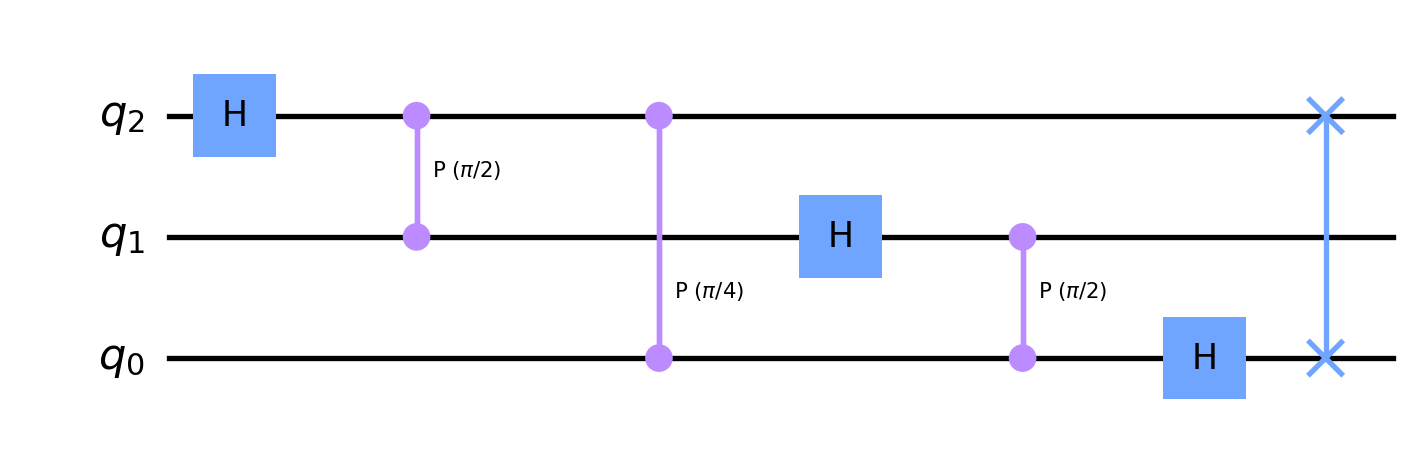
Similarly, we can plug the QFT-circuit above into the recursive formula 5 and (after expanding and simplifying) get \(QFT_4\) in terms of H, CP, and swap gates:
Code
qc = QuantumCircuit(4)
qc.h(3)
qc.cp(pi/2, 3, 2)
qc.cp(pi/4, 3, 1)
qc.cp(pi/8, 3, 0)
qc.h(2)
qc.cp(pi/2, 2, 1)
qc.cp(pi/4, 2, 0)
qc.h(1)
qc.cp(pi/2, 1, 0)
qc.h(0)
qc.swap(0,3)
qc.swap(1,2)
qc.draw(output='mpl', reverse_bits=True)
A couple QFT computations with qiskit
In the code blocks above, the recursive formula 5 was used to create the QFT-circuit with qiskit. The following shows how to perform QFT calculations with qiskit. First, lets check that our circuit correctly computes \(QFT_2|3\rangle\) (compare with 2 and 3).
from qiskit.quantum_info import Statevector
n = 2
a = 3
state_in = Statevector.from_int(a, 2**n)
state_out = state_in.evolve(qft(n))
state_out.draw('latex')\[\frac{1}{2} |00\rangle- \frac{i}{2} |01\rangle- \frac{1}{2} |10\rangle+\frac{i}{2} |11\rangle\]
For a slightly larger computation, let’s compute \(QFT_3|7\rangle\):
n = 3
a = 7
state_in = Statevector.from_int(a, 2**n)
state_out = state_in.evolve(qft(n))
state_out.draw('latex')\[\frac{\sqrt{2}}{4} |000\rangle+ (\frac{1}{4} - \frac{i}{4}) |001\rangle- \frac{\sqrt{2} i}{4} |010\rangle+ (- \frac{1}{4} - \frac{i}{4}) |011\rangle- \frac{\sqrt{2}}{4} |100\rangle+ (- \frac{1}{4} + \frac{i}{4}) |101\rangle+\frac{\sqrt{2} i}{4} |110\rangle+ (\frac{1}{4} + \frac{i}{4}) |111\rangle\]
Proof that QFT satisfies the recursive formula
To prove the recursive formula 5 we compute the output of the recursive circuit on an arbitrary \((n+1)\)-qubit representation of an integer: \(|a\rangle=|a_na_{n-1}\cdots a_0\rangle\). In doing so, it will continue to use the notation from Section 2.1.3 by writing \[ |a\rangle=|a_n\rangle\otimes|a'\rangle. \tag{6}\] Following 5, we first apply the Hadamard gate (which is \(QFT_1\)) to the left (top) qubit: \[ |a_n\rangle\otimes|a'\rangle \mapsto \dfrac{1}{\sqrt{2}}\sum_{0\leq b_0\leq 1}e^{\pi i a_n b_0}|b_0\rangle\otimes|a'\rangle. \] Next, (according to 5) we apply the CPC-gate to the result and use 4 to get \[ \dfrac{1}{\sqrt{2}}\sum_{0\leq b_0\leq 1}e^{\pi i b_0 a_n}|b_0\rangle\otimes|a'\rangle\mapsto \dfrac{1}{\sqrt{2}}\sum_{0\leq b_0\leq 1}e^{\pi i b_0 a_n}e^{\frac{\pi i b_0 a'}{2^n}}|b_0\rangle\otimes|a'\rangle. \tag{7}\] Since \[ 2^na_n + a'=a \tag{8}\] (which follows from 6), the exponentials in the output of 7 can be simplified as follows: \[ e^{\pi i b_0 a_n}e^{\frac{\pi i b_0 a'}{2^n}}=e^{\frac{\pi i b_0(2^na_n+a')}{2^n}}=e^{\frac{\pi i b_0 a}{2^n}} \] Thus, the output of 7 can be written as \[ \dfrac{1}{\sqrt{2}}\sum_{0\leq b_0\leq 1}e^{\frac{\pi i b_0 a}{2^n}}|b_0\rangle\otimes|a'\rangle. \] Next, (according to 5) we apply the QFT-gate to the right (bottom) \(n\) qubits using 1: \[ \dfrac{1}{\sqrt{2}}\sum_{0\leq b_0\leq 1}e^{\frac{\pi i b_0 a}{2^n}}|b_0\rangle\otimes|a'\rangle \mapsto \dfrac{1}{\sqrt{2}}\sum_{0\leq b_0\leq 1}e^{\frac{\pi i b_0 a}{2^n}}|b_0\rangle\otimes\dfrac{1}{\sqrt{2^n}}\sum_{0\leq b'<2^n}e^{\frac{2\pi i a'b'}{2^n}}|b'\rangle. \] If we write \(|b'\rangle=|b_nb_{n-1}\cdots b_1\rangle\), then the output above can be written as \[ \dfrac{1}{\sqrt{2^{n+1}}}\sum_{0\leq b_0,b_1,\ldots,b_n\leq 1}e^{\frac{\pi i b_0 a}{2^n}}e^{\frac{2\pi i a'b'}{2^n}}|b_0\rangle\otimes|b_n\cdots b_1\rangle. \] Now, (still following 5) we reverse the last (bottom) \(n\) qubits to get
\[\begin{align*} & \dfrac{1}{\sqrt{2^{n+1}}}\sum_{0\leq b_0,b_1,\ldots,b_n\leq 1}e^{\frac{\pi i b_0 a}{2^n}}e^{\frac{2\pi i a'b'}{2^n}}|b_0\rangle\otimes|b_1\cdots b_n\rangle \\ & =\dfrac{1}{\sqrt{2^{n+1}}}\sum_{0\leq b_0,b_1,\ldots,b_n\leq 1}e^{\frac{\pi i b_0 a}{2^n}}e^{\frac{2\pi i a'b'}{2^n}}|b_0b_1\cdots b_n\rangle. \\ & =\dfrac{1}{\sqrt{2^{n+1}}}\sum_{0\leq b_0,b_1,\ldots,b_n\leq 1}e^{\frac{\pi i (ab_0+2a'b')}{2^n}}|b_0b_1\cdots b_n\rangle. \end{align*} \tag{9}\]
Finally, if we let \(b\) denote the integer with \(|b\rangle=|b_n\cdots b_0\rangle\), then after we reverse all \(n+1\) qubits (the last step in 5) in 9 we get \[ \dfrac{1}{\sqrt{2^{n+1}}}\sum_{0\leq b_0,\ldots,b_n\leq 1}e^{\frac{\pi i (ab_0+2a'b')}{2^n}}|b_n\cdots b_0\rangle = \dfrac{1}{\sqrt{2^{n+1}}}\sum_{b=0}^{2^{n+1}-1}e^{\frac{\pi i (ab_0+2a'b')}{2^n}}|b\rangle. \] The state above the output of the recursive gate 5 applied to \(|a\rangle\). On the other hand, using 1 we get \[ QFT_{n+1}|a\rangle = \dfrac{1}{\sqrt{2^{n+1}}}\sum_{b=0}^{2^{n+1}-1}e^{\frac{2\pi i ab}{2^{n+1}}}|b\rangle. \] Thus, to complete the proof it suffices to show \[ e^{\frac{\pi i (ab_0+2a'b')}{2^n}} = e^{\frac{2\pi i ab}{2^{n+1}}} \] or equivalently \[ e^{\frac{\pi i (ab-ab_0-2a'b')}{2^{n}}} = 1. \]
Since \(|b\rangle=|b_n\cdots b_1b_0\rangle\) and \(|b'\rangle=|b_n\cdots b_1\rangle\), it follows that \(b=2b'+b_0\) so that \(b-b_0=2b'\). Using this fact along with \(a-a'=2^na_n\) (which follows from 8) we get the desired result: \[\begin{align*} e^{\frac{\pi i (ab-ab_0-2a'b')}{2^{n}}} & = e^{\frac{\pi i (2ab'-2a'b')}{2^{n}}} \\ & = e^{\frac{\pi i (2(a-a')b')}{2^{n}}} \\ & = e^{\frac{\pi i (2^{n+1}a_nb')}{2^{n}}}\\ & = e^{2\pi i a_nb'}\\ & = 1. \end{align*}\]